Deep Leanring with Tabular Data

TODO: Rough Notes on using Embeddings for Categorical Data

• Tabular Deep Learning uses techniques from Collaborative Filtering with Deep Learning

• It defines Categorical and Continuous Data/Variables

• Continuous Variables are things like age, data that is inherently expressed as a number and can be multiplied in matrix multiplication

• Categorical Variables are variables that are not inherently expressed as a number, or if it is a number, has no intrinsic significance for correleation finding e.g. a string or a numeric user id

• When it comes to training a deep learning model using tabular data, it combines the user embeddings from Collaborative filtering

• Categorical variables such as user id or item (“car x, car y” etc…) will have an Embedding create for each item

• An Embedding has a size/factor/number, it might look like this:

user_id_0 = [0.3, 0.2, 1.0, 0.5]
item_id_346 = [0.8, 0.3, 0.1, 0.2]

• A tensor/matrix of Embeddings will be generated, containing an embedding for every user and item.

• When it comes to training:

  • There will be a lookup for the embeddings based on the Categorical variable id
  • The Continuous variables can sometimes be passed to a separate linear layer
  • The embeddings of the Categorical variables and the output (if there was one) of the Continuous variables will be concatenated
  • They will be passed to the full linear layers like any other deep learning network

• When it comes to backpropagation:

  • After calculating the loss and the gradients
  • the gradients are in a tensor that reflect the size of the original concatenation
  • The gradient tensor is sliced according the size and positions of the original concat
  • The weights for each embedding and numerical values are updated according to the gradients
  • To be clear, every embedding for every item of categorical variables have their own weights

• SUMMARY: Embedding categorical variables TRANSFORMS categorical variables into continuous variables, allowing them to be used in the learning proccess

TODO: Modern Machine Learning

• Studies have shown the majority of datasets can be modeled with just two methods:

1. Ensemble of decision trees (random forests, gradient boosting machines) - mainly for structured data (like database tables)
2. Multilayered neural networks learned with SGD, mainly for unstructured data (audio, images, natural language)

For strucuted data, both can be used and tend to give similar results but ensemble trees tend to train faster. They don’t need special GPU hardware at scale and require less hyperparameter tuning.

TODO: Step by Step notes

• We converted the column that has the target data by the natural logarithm to reduce the scale and the relative variance of the calculations. This should be done on targets that will use RMSE?

Decision Trees

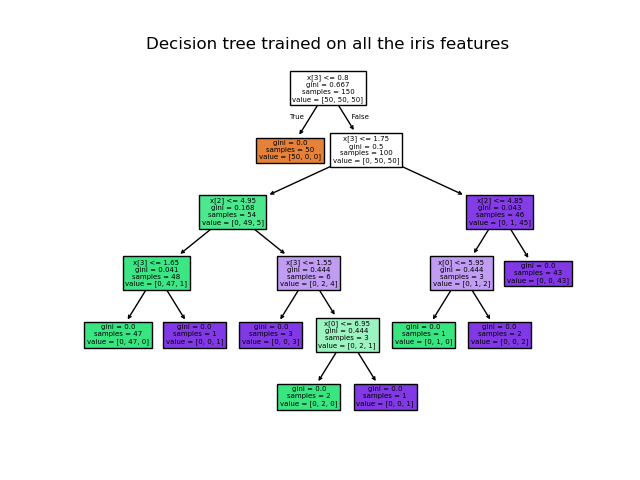
Decision trees are a data structure to model a dataset. It’s essentially a binary tree that splits the data into groups by asking a series of binary question (true or false).

How the tree is split depends on impurity functions: Gini Impurity, Entropy or Mean Squared Error.

Decision Trees decide the split by finding the threshold of a feature that results in the lowest impurity or highest information gain.

Steps

1. Splitting the data (threshold)

• The root node starts with all the data, it goes through each feature and threshold per category.

• The questions that are generated for the split, takes ALL the unique features for numerical variables and categorical variables and calculates the impurity.

• For numerical fetures like age and income, the algorithm will go through different values to find the best threshold e.g.

Age < 30
Age < 40
etc ...

• For categorical variables, they can be split by asking questions:

Is Gender = Male?
Is Gender = Female?

2. Evaluating the quality of the split

The algorithm then evaluates the quality of the split.

For Classification

Gini Impurity

$ Gini(t) = 1 - \sum_{i=1}^{C} p_i^2 $

• Measures how mixed the classes are at the leaf node

• A low gini impurity means that if the node contains more of the same classes, its pure

• Example:

  • If a node contains 80% of one class and 20% of another class, the gini impurity is low
  • If a node has an even distirbution of classes, the gini impurity is high

• It’s important to note, the split and gini impurity is against the target variables NOT the feature variables.

$ p_i^2 $

$ p_i = num_i / numsamples $

• p_i is the portion of the class i in node t. This is caluclated by taking the number of i and dividing it by the number of samples in the node

$ 1 - \sum_{i=1}^{C} $

For every sample (every class) in the node, apply p_i^2, add them together and then subtract one from the product.

Entropy

$ Entropy(t) = - \sum_{i=1}^{C} p_i \log_2(p_i) $

• Same principle as Gini Impurity
• If the product of the Entropy calculation is 0, then all samples belong to the same node

Mean Squared Error - Regression Tasks

$ MSE(t) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y})^2 $

• MSE (Mean Squared Error) is used to measure the quality of the split based on the variance in the subset.

1. Split the dataset according to a threshold, e.g. split into two subsets “age <= 30”

2. In each subset, calculate the mean of the target variable

TODO: Get the Latex

subset mean = sum of target values in subset / number of items in the subset

3. Calculate and sum the squared error for each item

TODO: Get the Latex

squared_err_i = (actual item value - subset mean)^2
squared_err_sum = sum(all squared_error_i)

4. Calculate the Mean Squared Error for each subset

TODO: Get the Latex

subset_mse = squared_err_sum / num_items_subset

5. Calculate the weight of the MSE for each subset

weighted_mse = num_items_subset / num_items_dataset * subset_mse

6. Sum the weighted mses for the split to get the total MSE

total_mse = sum(weighted_mse)

If the total MSE of the subset splits are low, meaning the split is pure. It means each subset has low variance of items in each split.

• MSE has been covered in previous articles, but here is a quick review:

$ y_i $

• Is the true value

$ \hat{y} $

• Is the predicted value for the i-th sample

$ n $

• Is the number of samples

3. Choosing the best split

• For classification - the best split minimzes the impurity
• For regression - the best split minimizes error

4. Recursive Process

Once the split is made, it will recursively repeat the process for the child nodes

• For each child node, it will pick the feature and threshold that will best separate the data

5. Stopping criteria

The recursive algorithm will stop according to one of the stopping criteria:

• Maximum depth of tree has been reached
• Minimum samples per node (the minimum number accepted in a node before attempting another split)

Decision trees are a fundemental datastructure in Machine Learning. They are computionally simpler than neural networks but are prone to overfitting.

Random Forest

A Random Forest is an ensemble (collection) method of decision trees.

Random Forests are a machine learning technique to improve the quality of predictions and generalizations compared to a single decision tree.

Random Forests take a random subsection (random sampling) of a dataset and creates a decision tree for that random subsection. The decision tree also takes a random subset of features. This is applied x number of times across multiple decision trees. The randomness ensures that each decision tree covers at different subsection, leading to improved generalization. This is known as “Bagging” or “Bootstrap Aggregating”. Also important to note, the random sampling is with replacment, meaning the item is not taken out of the training data. This means that other trees may have an overlap and this is important in building a model that can generalize.

When a prediction needs to be calculated, it will run it through all the decision trees and take an average of the result for regression tasks and for classification a majority vote.

The output is a more generalized result that is less prone to overfitting.

Out of Bag Error

Out of Bag Error is a way to validate the Random Forests Prediction. This is because each Decision Tree has a randomized subset of the data, therefore there are rows of data that are not included in the Decision Tree. The missing data acts as data for a validation set.

To measure the accuracy of prediction, rows that were not included in the Decision Trees dataset are used to measure the error rate of the prediction. This is still applied to all of the Decision Trees and the average or majority vote is used in the error rate calculation.

Variance in Predictions

Since a Random Forest uses an ensemble of decision trees, it is important to determine whether the model has confidence in the predictions. This is achieved by measuring the standard deviation of the Random Forests predictions. If the standard deviation is high, then the Random Forest is not very confident in its prediction as the ensemble of trees will have different views on the prediction.

A high variance should initiate caution when using the prediction.

Feature Importance

This is a useful technique for understanding which features have the highest impact in predictions in the Random Forest.

This allows us to gain insights on how the tree splits the data by most important features and also gives us insights into understanding the problem domain. It also allows us to remove the less important or redundant features since this can lead to simpler models and better generalization.

Data Leakage

Usually happens with there is a lack of information or missing data or the target variable is used as a feature in training.

An important part to prevent data leakage is to make sure the target variable/feature is NOT included in the the training. It must ALWAYS be the y variable. If its included in the training, the model will essentially “cheat” and overfit.

Another way data leakage can occur is when using “future” data points, which may seem impossible. But in time series data, rolling averages can cover a span into the future. This data can be inadvertenly used in model prediction that can influence training. It’s important to only use data that fully ends at a certain point in the past.

Its usually better to check after the model is trained because the signs of data leakage are:

• The accuracy of the model is too good to be true
• Important predictors that don’t make sense in practice e.g. people that submitted grant applications on jan 1st all got approved and everyone who didn’t got rejected
• It’s better to build the model and then do data cleaning/normalization. This way you’ll clearly see any data leakage or ways to optimize

Extrapolation Problem

The Extrapolation Problem is when a Random Forest or any type of Machine Learning model needs to make predictions outside the range of values in which the model was trained on. It will very likely provide a prediction undert the expected range/value.

Detecting Out of Domain Data

The Extrapolation problem establishes that Random Forests are unable to make accurate predictions outside its trained range of values.

To detect whether a Random Forest has an Out of Domain problem, e.g. the validation and/or test data has wildly different data from the training data (meaning the training data will never be able to accurately predict the values in the validation set). We train the Random Forest on the training data, use a prediction from the validation or test data and determine the confidence of the predictions across the ensemble of trees.

If the confidence is low, then this is potentially detecting out of domain data.

• For regression, its the variance of the predictions across the trees. Using the standard derivation.
• For classification, its the spread of predicted class probabilities

Another strategy is to combine the training and validation set and add a is_test column for the validation/test training set. Train the model. If the error rate is high it means the model can’t tell the difference between the trianing and validation data meaning the both the training and validation data are in the same domain. If the error rate is low, then the two data sets are different domains.

If the error rate is low, then we can find the most important features. These features are what distinguishes the two data sets. If we remove them, then we can take steps toward a model that can generalize.

e.g. if you have a dataset where all the healthy plants are in blue pots and all the unhealthy plants are in red pots. The model might just look at the pots to determine whether the plant is healthy or not instead of the plant itself. By remove that feature, it forces the model to look for the underlying patterns in the plant itself.

We can then calculate the RMSE to get the error rate. If we try removing some ofthe higher feature importance columns and try to run the training agian and lookup the RMSE, we can remove see which columns are important and the ones that are introducing noise and bias. For example, Categorical IDs of usres or maybe some items that don’t contribute to identifying the underlying pattern with target variable could be removed.

Also, maybe removing very old data where the relationship is no longer valid can also help reduce the noise and bias.

Gradient Boosting Machines

Boosting is a technique that can be used in Random Forests as oppossed to bagging.

Instead of being trained on random subsets of data, each tree is trained on the whole dataset.

The first tree is trained and the difference between the targets and predictions, called the residuals. The residuals are used as the targets in the next tree.

The next tree will try to improve on the errors of the previous tree. This continues until a stopping point.

Boosting can be more accurate than bagging but has higher risk of overfitting.

Neural Nets with Tabular Data

Uses Embeddings for categorical variables

Did you find this page helpful? Consider sharing it 🙌