Neural Networks 101: Part 1 - Basic Overview

This post is purely a high level overview of Neural Networks. The goal is to conceptually understand Neural Networks and how they work.

What is a Neural Network?

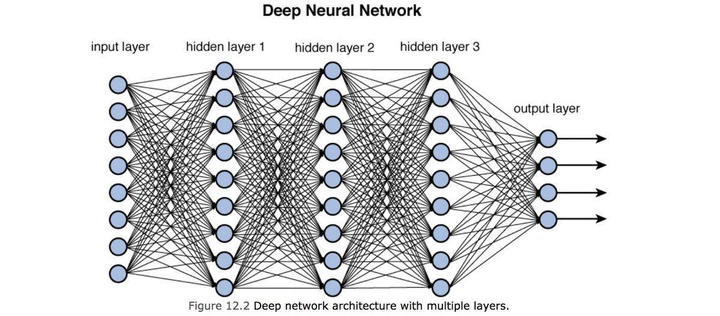
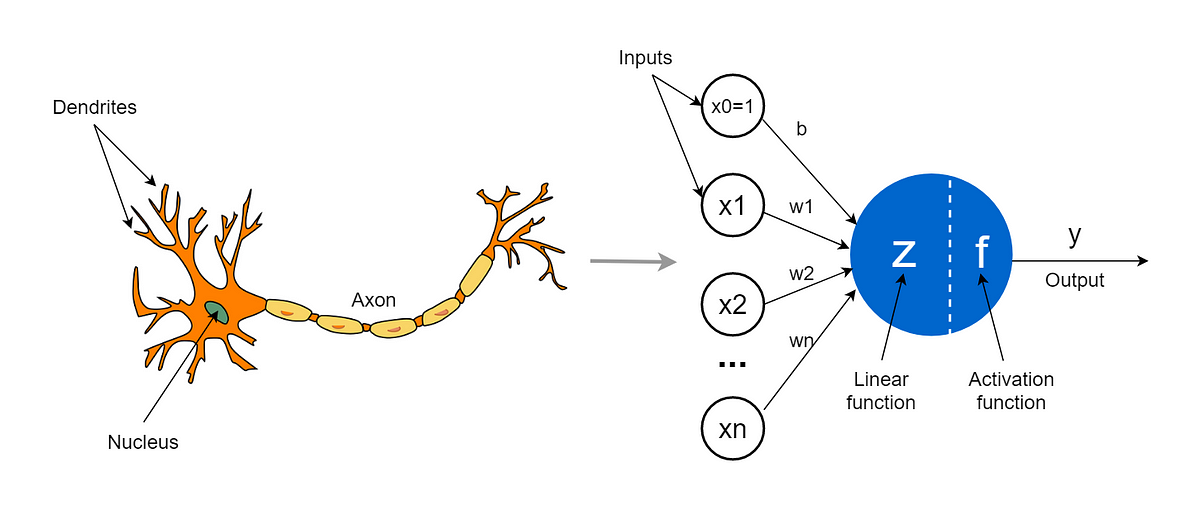
A Neural Network is a mathematical architecture that models the neurons in the human brain.

To put it simply, a Neural Network is made up of neurons. These neurons take input and produce an output.

In practice, a Neural Network is an architecture that allows a computer program to learn on its own to solve a particular problem.

It wasn’t until the 1980s where developments in the field of PDP (Parellel Distributed Processing) outlined a guide to improve Neural Networks and Machine Learning, based on the cognitive process:

A set of processing units

A state of activation

An output function for each unit

A pattern of connectivity among units

A propagation rule for propagating patterns of activities through the network of connectivities

An activation rule for combining the inputs impinging on a unit with the current state of that unit to produce an output for the unit

A learning rule whereby patterns of connectivity are modified by experience

An environment within which the system must operate

The modern approach to Neural Networks is very similar to the approach used described in the 1980s using PDP.

Modern Neural Networks

To understand Neural Networks at a high level, we need to understand how computer programs work at a high level.

Here is the basic idea of a computer program:

Neural Networks still follow this basic concept of a program. Given inputs into a program, it should emit outputs.

Neural Networks begin to diverge from typical computer programs when it comes to understanding the relationship between inputs and outputs.

To simplify the understanding of the difference between Neural Networks and computer programs, I’ll explain at a high level, how Neural Networks work.

High Level: How Neural Networks work

A Neural Network will be shown input data, along side the correct and corresponding output data.

The Neural Network will have to “remember” this connection/relationship.

The Neural Network will then be shown other input data WITHOUT the correct output data.

The Neural Network will be asked to calculate the correct ouput for the given input WITHOUT knowing or seeing the correct corresponding output.

The Neural Network will need to use its knowledge of previously seen correct input and output connections, and make a calculated guess to the correct output.

So far, we’ve explained conceptually, how a Neural Network differs from a traditional computer program. It learns relationships between certain inputs and outputs, and then is asked to calcuate outputs of unseen inputs.

In the next section, we’ll go into detail on how this “learning” process is achieved.

How Neural Networks “learn”

First, let’s ask our selves, why use Neural Networks instead of traditional computer programs?

In regular computer programs, the programmer must declare every single step on HOW to achieve a certain output. For extremely difficult problems such as, telling a computer how to recognize an image. The programmer would need to write an incomprehensible number of conditional statements, such as if this pixel, then this, but if the pixel is that then this, but if one pixel follows another then it could be this etc…

Our brains recognizes images intuitively, but there must be so many different variations and cues to come to the conclusion of classifying an image.

Neural Networks are modelled like our brain to “learn” by itself, therefore the programmer does not need to account for every single possible condition, instead, the programmer sets up an environment for the program to learn and recognize all of these conditions.

Arthur Samuel on AI:

Suppose we arrange for some automatic means of testing the effectiveness of any current weight assignment in terms of actual performance and provide a mechanism for altering the weight assignment so as to maximize the performance. We need not go into the details of such a procedure to see that it could be made entirely automatic and to see that a machine so programmed would “learn” from its experience.

Arthur Samuel was a Computer Scientist and one of the early pioneers of AI/Machine Learning. He famously wrote an early Machine Learning program that learned to play checkers to an amateur level.

Let’s extract some concepts from the quote:

1. The idea of a “weight assignment”
2. The fact that every weight assignment has some “actual performance”
3. The requirement that there be an “automatic means” of testing that performance
4. The need for a “mechanism” (i.e., another automatic process) for improving the performance by changing the weight assignments

We can reimagine the neural network “model” as such:

Weights are now an important variable. They allow us to make adjustments (automatically) on how the program will operate on the input in order to improve the output.

Lets update our diagram again to change Program to Model, and Weights to Parameters, this is to reflect modern terminology and importantly, weights will be reserved for a particular type of model parameter.

In order to adjust our Parameters, we need a mechanism to assess the output and automatically adjust the Parameters based on the performance.

In Samuels case, the outputs were assessed according to how the checkers model played against another model, the Parameters would then be adjusted towards the winning model.

We need to add another variable, PERFORMANCE. Notice that OUTPUT, is different from PERFORMANCE.

PERFORMANCE is the measurement of the accuracy of the OUTPUT. The model needs to update the PARAMETERS according to the PERFORMANCE NOT the OUTPUT.

We can see that:

• Both PARAMETERS and INPUT are given to the MODEL to produce an OUTPUT
• We measure the accuracy of the OUTPUT in the form of a PERFORMANCE
• We make updates to the PARAMETERS according to the PERFORMANCE in the effort to increase the quality of the OUTPUT

This is the process in which a Neural Network “learns”, by automatically and iteratively adjusting parameters that will influence the performance of the model, according to past performance.

Lets complete the diagram using accurate terminology.

• MODEL to ARCHITECTURE
  • The MODEL refers to the broader picture including the ARCHITECTURE, INPUTS and PARAMETERS
  • The ARCHITECTURE is the actual function in the neural network, It describes:
    • The layout of the network
    • How the neurons are organized
    • How many layers the network has
    • How many neurons are in each layer
    • The type of activation functions and how they are connected (the topology of the network)
• OUTPUTS to PREDICTIONS
• Add LABELS (used to measure the loss)
• PERFORMANCE to LOSS
  • The LOSS not only depends on the PREDICTIONS but the LABELS (what the prediction should be)

Summary

Neural Networks are a mathematical architecture that model neurons in the human brain. In practice, Neural Networks are form of computer program that is capable of “self learning”.

Neural Networks predict a certain output when given a certain input.

Neural Networks “self learn” or “self improve” using an automatic mechanism of adjustment.

Neural Networks “self learn” by:

• Using values for parameters and a given input
• The parameters and input are passed to the architecture
• The architecture produces predictions (expected output)
• A loss is calculated (in otherwords the accuracy of the prediction against the corresponding label)
• The parameters are adjusted according to the loss
• The process repeats until the loss is at a satisfactory level, meaning the model has learned to make predictions with accuracy

In Part 2, we’ll go into detail on the Maths behind Neural Networks.

Did you find this page helpful? Consider sharing it 🙌